
APPENDIX A: DATA SETS USED IN THIS HANDBOOK. Methods and formulas for confidence intervals and bounds in. ADDITIONAL TOPICS IN ANALYSIS OF VARIANCE. Methods and formulas for confidence intervals and bounds in Binomial Capability Analysis. we see that our calculated sum of squares for error matches Minitabs. Making the Table and Computing Chi-Square. Question 4 4 pts if we want ton construct 90 Confidence Interval for the Slope B1. Interpreting Residuals in Simple and Polynomial Regression. The confidence interval indicates that you can be 95 confident that the mean for the entire population of light bulbs falls within this range. Making Inferences from Straight-Line Fits. Minitab calculates that the 95 confidence interval is 1230 1265 hours. Each example and exercise is broken down into the exact steps that must be followed in order to take the reader through key learning points and work through complex.
#MINITAB CONFIDENCE INTERVAL HOW TO#
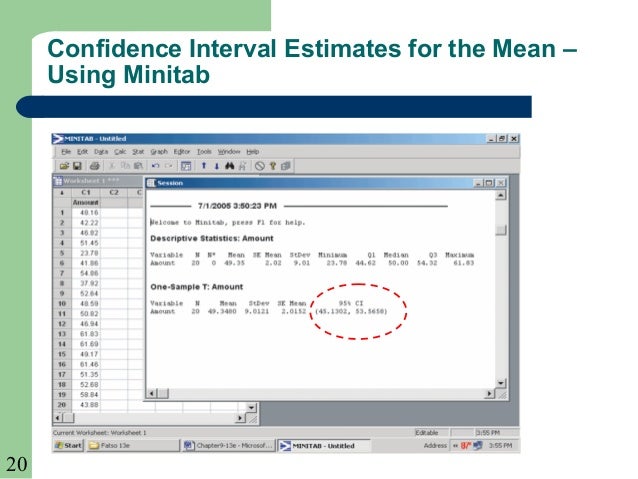
Minitab Constructing a Confidence Interval with Summarized Data Lets estimate. Problem Solving and Data Analysis using Minitab presents example-based learning to aid readers in understanding how to use MINITAB 16 for statistical analysis and problem solving. We would be 95 confident that auto insurance premiums in Michigan are above. The 95 confidence interval for Michigan does not include the national average of 1503 for the the national average States.
#MINITAB CONFIDENCE INTERVAL SOFTWARE#
Simple Regression: Fitting a Straight Line. Minitab - Statistical Analysis Software - Library Guides at Penn State. 95 confidence interval: x t ( s / n ) df 19 2551 2 (301 / 20) 2551 141 or 2409 to 2692.
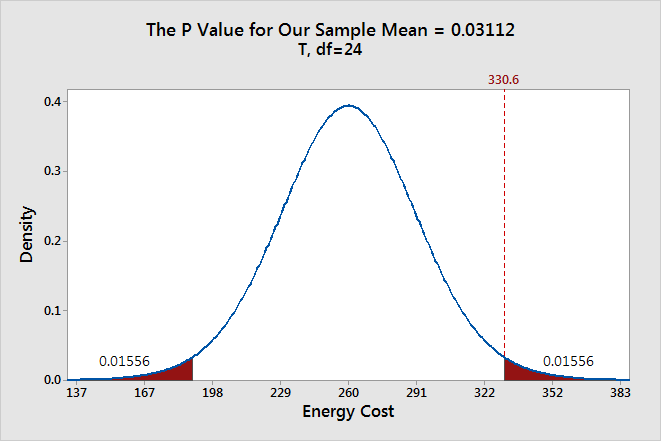
of using Minitab to find the p-values for given F test statistics. Difference Between Two Means: Independent Samples. true ratio of variances is not equal to 1 95 percent confidence interval: 0. Difference between Two Means: Paired Data. COMPARING TWO MEANS: CONFIDENCE INTERVALS AND TESTS. for a 98 confidence interval with 15 degrees of freedom: In Minitab. Confidence Intervals and Tests for Proportions. For example, if you want a t -value for a 90 confidence interval when you have 9. ONE-SAMPLE CONFIDENCE INTERVALS AND TESTS FOR MEANS. The Base for the Random Number Generator. mathematical statistics, topics include an intuitive presentation of the (single and double) bootstrap for confidence interval calculations, shrinkage estimation, tail (maximal moment) estimation, and a variety of methods of point estimation besides maximum likelihood, including use of characteristic functions, and indirect inference. Simulating Data from Other Distributions. Simulating Data from the Binomial Distribution. In Minitab, to display the Prediction interval (PI) in a graph go to Stat > Regression > Fitted line Plot. Simulating Data from a Normal Distribution.
A Summary of the Theoretical Distributions in MINITAB. Summarizing and Displaying Categorical Data. ONE-VARIABLE GRAPHS AND SUMMARIES.Understanding Variable Types. Working with the Contents of the Session Window. N = total number of observations = ∑ m = the sigma tolerance value (6 by default) Rspan = the length of the moving range (2 by default) is calculated as follows, according to the method you choose to estimate within-subgroup standard deviation (pooled standard deviation is the default) Pooled standard deviation � � � i Rbar ( �1) n v �.

⁄ ̂ ⁄ = the (1 – α/2) percentile of the standard normal distribution ni = the i th subgroup size k = the number of subgroups n = the average subgroup size = ∑ if n is not an integer, round it up to the closest integer.
Capability Analysis (Normal Distribution) Formula for a (1 – α)100% confidence interval for Cp: Technical Support Document Confidence Interval Formulas for Cp and Cpk ̂ √ Formula for a (1 – α)100% confidence interval for Cpk: Where: ̂ ⁄ √ ⁄ ̂ ̂ = the estimate of Cp calculated from your data ̂ = the estimate of Cpk calculated from your data Knowledgebase ID 853: ̂ √ ̂ ⁄ √ = the α percentile of the chi-square distribution with υ degrees of freedom.


 0 kommentar(er)
0 kommentar(er)
